What is big O?

In computer science, big O Notation is the term used to describe the performance and complexity of an algorithm as the input size is increasing.  Basically, it is the number of operations It would take for an algorithm to execute when passes some input. Programmers use big O notation to analyze the time complexity of an algorithm.  It is used to have a high-level overview of how efficient an algorithm is and it gives a way to compare the efficiency of algorithms in solving complex problems. 

The need for Big Notation 

In programming, it is possible to implement the same solution in many different ways.  Sometimes we need to compare several implementations to determine which one performs better.   You can use a time clock to measure how long a program would take to run.   The caveat with this approach is time clock is not very reliable because it is hardware dependent. 

The time the program will take to run is highly dependent on the computer hardware such as CPU, memory, or maybe just waiting for a new thread to be open.  This is where big O notation comes into play. It only considers the number of operations the program would take in the worst-case scenario. 

For example, if we have a list of 20 elements and we want to find a specific element in the list.  The best scenario is the element we are looking for is at the beginning of the list.  In this case, it only takes one operation O(1) (constant time ).  The worst-case scenario would be if the element is located at the end of the list or maybe it is not even in the list. 

The number of operation will depend on how many items is on the list because we have to traverse all of them to find the items or to confirm it is not on the list. In this case, the big O would be O(n) meaning it takes n operations to find the item in the list. 

It is important to remember big O notation only cares about the worst-case scenario. Here is some of the most common complexity. 

• Constant time or O(1)
• Linear time or O(n)
• Logarithmic time or  O(n log n)
• Quadratic time or O(n^2)
• Exponential time or  2 ^{polyn}
• Factorial time or O(n!)

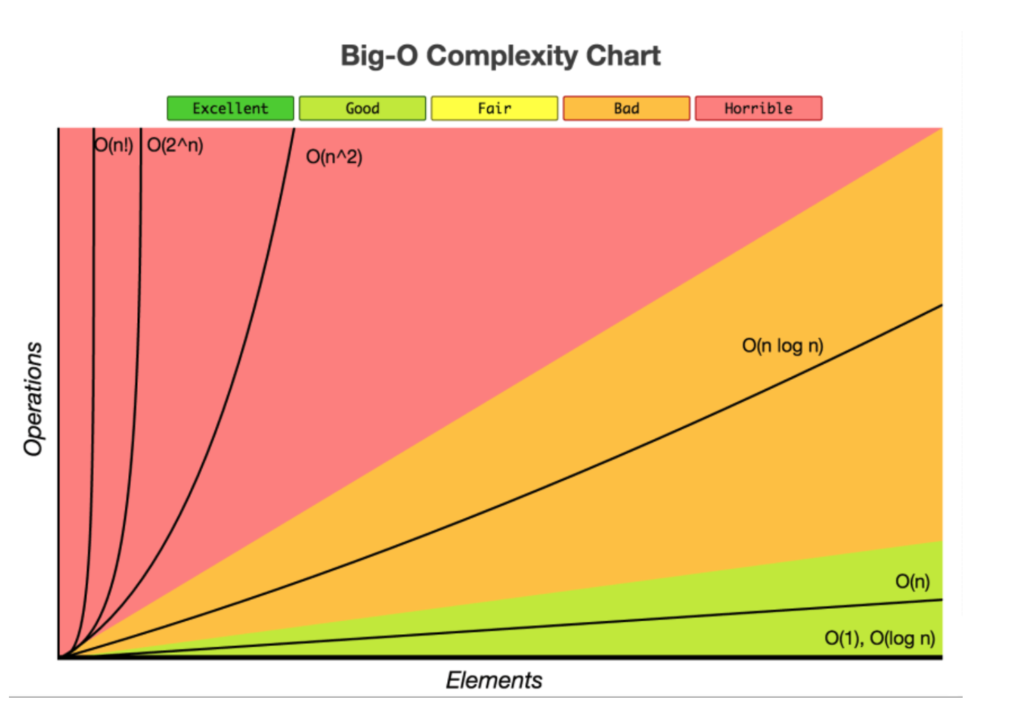
Here is a summary of big O notation.

Constant time or O(1)

O(1) or constant time describes an algorithm that will always perform the same amount of operations no matter what the input size is.  Because there is no dependency between the number of operations and the input size, the runtime will remain the same.  For example, printing the 5th element in a list of 10 elements.   It does not matter if the list has only 10 elements or 20000. There will always have the same amount of operations. 

students= ['Patric', 'Marc', 'Alex', 'Jean', 'Sarha', 'Robert', 'Nalby', 'Rose']

def get_student_name(name, index):
    print("the student's name is: " + students[index])
    
get_student_name(students,4)

# Big O(1)

Linear time or O(n)

Linear time complexity or O(n) is used to describe an algorithm that the number of operations will increase proportionally to the size of the input. For example, print all elements in a list. 

Input = 1   operation =1

Input = 20   operation =20

Input = 1000   operation =1000

def printing_name(list):
    for name in list:
        print(name)      

#Big O(n)

Logarithmic time or  O(log n)

Often referred to as divide and conquer algorithms. In a logarithmic time complexity algorithm, the number of operations does not increase proportionally to the increase in the input size. This algorithm is widely used in sorting. A good example would be binary search.

Log-linear complexity or O(n log n)

Often log-linear complexity is found in algorithms that implement some sort of recursive call.  It means that the number n operation will be called n times during the execution of the algorithm.  A good example of that would be a binary tree sort. 

Quadratic time or O(n^2)

Quadratic time complexity describes an algorithm when the number of operations is directly proportional to the square of the size of the input. For example, if there are 2 nested loops. The complexity will be n^2

def greeting(number):
    for i in range(number):
        print('Hello from the outside')
        for j in range(number):
            print('inside loop')
            
            #big O(n^2)

Exponential time or  2 ^n

Exponential time complexity is often found in algorithms where there is a recursive call.  The number of operations doubles as the input size increases. A good example would be the Fibonacci sequence algorithm.

def fibonacci_sequence(num):
    if num < 0:
        print('incorrect number')
    if num == 1 or num ==2:
        return 1
    last = fibonacci_sequence(num - 1)
    second = fibonacci_sequence(num -2)
    return last + second

Factorial time or O(n!)

Factorial time complexity is one of the least efficient in terms of the number of operations because the output of this algorithm will be multiplied by factorial. A good example would be the traveling salesman problem. 

Algorithm big O notation summary

Source: Big O Cheat Sheet